Earth Null School Follow Up: Is Greenland Bigger Than Brazil? UPDATED For Images

[UPDATED:  I've redone the images, so they should be visible this time.  Sorry.]

Former Alaskan and aviation faculty member and a pilot, Bill Butler, offered some followup info and images to my Earth Null School post.  I asked if I could post his email as a guest post.  He graciously agreed.  So here's a little more on this topic, which because it deals very visually with distortions of "how we know," is very dear to this blog's underlying theme.
I'm told, that geography isn't taught much in school these days.  My sense is that there are people who really, really know this stuff, people like me who sort of know it, and then most other people who don't have a clue.

With GPS people don't even need to read maps at all any more.  But understanding this helps us understand other geo-political issues.  Plus maps are a good metaphor for other representations of reality that aren't as tangible - like words and theories. And this issue about Mercator projections and how they distort size is certainly important to Alaskans.  (Relax, even after undistorting us, we're still bigger than Texas.)

So, for those of you for whom this is a stretch,  I invite you to do a little mental yoga.   I'm also trying to use parts of my brain that usually don't have to move at all.  And so, you'll see at the end of this post, my questions to Bill, and his further response.  

Part I - Bill's Guest Post

Because Mercator "straightens" the meridians of longitude, making them appear parallel instead of converging at the poles, he needed to mathematically stretch the distance between the parallels of latitude to keep proper relations between two points in the same region and then slice open the resulting cylinder to make a flat surface.  Note how the squares (known as graticules) become rectangular toward the poles.  The distortions are huge and obvious when we hang a map of the world on the classroom wall, but if our object is to make an accurate map for a voyage from, say--Norway to Scotland--they are insignificant :

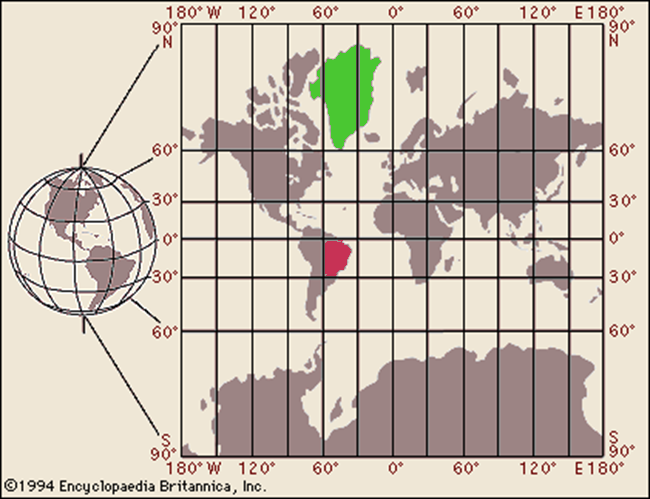
[Steve's note:  Greenland (green) is mostly between 0˚ and 60˚ W and between 90˚ and 60˚N.  Brazil (red) is between 30˚ and 60˚W and 0˚ and 30˚ S]


On Mercator's Projection, the only place where there is no distortion is along the equator.  The farther you move from it, the greater the distortion.  The traditional comparison is Greenland to Brazil.  Brazil is 2.5 times the size of Greenland, but if you are navigating from Thule to Godthaab, that doesn't matter.

Johann Lambert (1728-1777, an Alsatian) figured out that if instead of creating Mercator's cylinder, you built a cone, it could also touch the surface at some parallel other than the equator and that would be the circle of zero distortion, and by moving the apex of the cone up or down in theoretical space you could choose whatever parallel suited the cartographer's need.  The flattened shape is awkward, but if you are making a series of smaller charts, they can be made in the traditional square or rectangular formats :





Further, Lambert discovered that you could project your cone through the Earth's surface and "touch" at two reference parallels with very little distortion:




You just sort of "tamp down" the bulge of the earth between the "standard parallels" and ignore the very small distortions, as in this example (note the bottom of the legend):






Here's a common use of Lamberts.  The table at the bottom of the legend shows the series of charts, using a variety of "standard parallels" to assure  the minimal distortion.  The lack of distortion in the Lambert projection is especially important for aerial navigation because it permits us to draw a straight line on the chart which is truly represents a great circle on the spherical earth, and great circles are the true path of the radio waves we use to establish positions and courses:




Pedantically yours,

Bill Butler
Professor of Aviation Technology (retired)


PART II - Steve's Questions and Bill's Response

Steve:  Can you explain a little more about the Lambert Charts?  Like, what are they for?  Who uses them? 

Bill:  Actually, they are used for a lot of things, but aircraft navigation may be most common  They come in different scales and with differing levels of detail, but their use is universal, and even with electronic mapping in most airline cockpits, these are the charts which are digitized.  The curved parallels of latitude are a natural outcome of projecting a sphere onto a flat surface, but they are only obvious over a great distance.

Steve:  Why does it say north to the right and south to the left when the map looks like those should be east and west?  Could use a more current one?
 

Bill:  What you are looking at is the cover of an aeronautical chart, where the legend appears explaining what is inside.  "north/south" tells you that this is a two-sided document and if you unfold it from this edge... 

Steve:  Why does it say Seattle, when it has the whole northern part of the US on it?

Bill:    It [the map below] says "San Francisco", for reasons which seem obvious...at least to me [;->  It is one of a set covering the entire nation and the little map shows you what all the others are named.  Note that the Lambert standard parallels for this chart are different than the ones used for the Seattle chart.




Steve:  OK, this is the cover page of your map.  And the little map that is cross hatched - in this case San Francisco - is what is inside this cover.  And in the previous map, I now see that Seattle is also cross-hatched. And thus the north and south designations on the sides would make sense when I opened the map.  Right?

Bill:  Exactly


Bill:  Let me back up a bit to Mercator, who shows that any "great circle" can be projected without distorting it.  He did this mathematically, but graphically, it looks like a sphere within a cylinder.  Note that the when the sphere was inflated to contact all points of the cylinder, only the equator stays exactly where it was, i.e. undistorted.  Now the meridians, while bent, retain their spherical nature, just like the equator.  That is, if you draw a straight line from say Kodiak to Hilo, it is truly the shortest distance and undistorted because they are both on the 150th Meridian, but if you draw a line from Anchorage to Oslo on the map below, even they are both roughly on the 60th Parallel, the track is hugely distorted, because as we both know, the shortest way is over the north tip of Greenland:





This problem can be attacked by what is known as a Transverse  or Oblique Mercator, that is by rotating the sphere within the cylinder so that any line we choose is a "false equator, that is, the line of zero distortion.  This is actually how Pan American attacked the problem when they began flying long overwater routes in the mid-30s; they would make special charts specific to each route and the crew could plot out their course knowing that what was on the paper was the shortest line between two points on a sphere, i.e. a great circle:




This solution is unworkable in a system where tens of thousands of aircraft fly hundreds of routes every day, but Lambert, provides the solution because we can use his theoretical cone (cones, actually, because we choose the one which touches the surface in the zone we are interested in) to map the entire earth with parallels, meridians and course lines drawn to look straight on the flat paper.  This is what the inside of that Seattle aeronautical chart looks like.  I have drawn a line from Portland to Boise in this example:





Notice that the meridians and the parallels appear to be straight (well, the parallel does show a bit of bend, but the error induced is miniscule), although they are segments of a great circle.  Lambert's genius is that the cartographer can select any "standard parallel" for zero distortion, and when he makes the next map to the south or north, choose a different parallel (actually two are used for each chart with acceptable error).

Steve:  Let's see if I got this.  With the original Mercator charts, you're saying, if you just focus on a small portion, even though there is distortion away from the equator, the distortion is the same throughout that small portion, so it's still usable.  Is that right?

Bill:  Almost.  There is a difference between the drawn line and the great circle which truly represents the shortest distance, but an 18th century sailor who was going from Newcastle to Bergen, unless he understood the spherical geometry (unlikely) would be unaware of any error, except it would take him a bit longer than he thought it should.  If he was sailing from Cardiff to Cadiz, there would be almost no error at all because the north-south meridians drawn as straight lines are still great circles.  Generally speaking, these errors were inefficient, but harmless until we started navigating over great distances in short times and using radio to determine courses and positions.

Steve:  And Lambert, by changing the "equator" for each map, clears the distortion that way?

Bill:  Exactly.

And I'm sure Bill would be glad to answer further questions in the comments.

Capturing El Chapo

The LA Times had a front page story today about the capture of Mexican [I'm paused here trying to think of a word other than 'drug lord' or 'drug kingpin'] pharmaceutical company CEO, Joaquin Guzman.   OK, I know that's a bit of a stretch, but drug companies in the US have a huge amount of sway over the government here, just as Mr. Guzman did in Mexico.  And they've got lots of people on lifetime commitments to their products.  They just do it in a more civilized manner and with incorporation papers and appropriate laws that make most of what they do legal.  And their compensation isn't that far behind Guzman's and they have a lot more respectability. 

For the record, here are two men from the top paid US CEO's from a 2011 Daily Mail article:

"The top spot is held by John Hammergren, 52, the CEO of pharmaceutical company McKesson who earned a salary of $131.2million and a net total income, which includes bonuses and profits from stock earnings, of $1.2billion. And that's not all: Mr Hammergren's company stands to expand if President Obama's health care program is enacted due to increased contracts. . .

Number 8: Stephen Hemsley

CEO of UnitedHealth Group, Health care
Compensation: $48.8million
Net Income: $4.93billion"

Whoa!  Where did that come from?  All I intended here was to point folks to a documentary about Guzman that I posted Feb. 14.  I was giving an example of what you could find on Documentary Heaven, and it was the only one I had actually watched. 

It will fill in a lot more details of this person's life, the incredible wealth (they found $200 million in cash when they raided his palace), and how he ruled with a mix of carrot and stick.  And, most certainly, his organization uses the same methods here in the US.  If you were a judge and you were offered to have your debts taken care of for your help and this offer also included pictures of your kids and grand kids if you don't help, you surely would pause before making a decision.

Anyway, I thought I'd redirect folks to the video, now that his name is back on the front pages. 

The LA Times article both says the arrest is significant and that it will have no affect on the operations of the Sinaloa drug cartel. 

Working Hard To Get Back To The Start - Tag Your Luggage, And Richard Powers' Orpheo

Sometimes you have to work to just get back to where you started.  Most of this was my own fault.  It began Wednesday night at my mom's house when I opened my suitcase and found out it wasn't mine.

I called Alaska Airlines and related how someone had handed down my carry-on suitcase from a row or two behind and I hadn't looked at it carefully as people were waiting to get off.  I had the name of the person whose suitcase I had, but she said he wasn't listed on the flight.  And no extra suitcases were found either.  Uh oh.  Did I mix it up in the bathroom? Or on the shuttle bus?  

I called OP (other passenger), but there was no answer or voice mail.  I emailed him and went to bed.  He called the next morning, relieved that his suitcase was safe and said that the shuttle driver had taken mine to lost and found.  I called the shuttle company, they gave me another number, but they didn't have it, but gave me another number.  Nor did they.  But they gave me yet another number (the lost and found of the shuttle service whom I called in the first place) and they had it. 

I got into my mom's car to get my suitcase, but it wouldn't start.  I borrowed another car.   When I got there and told her who I was, the woman said that someone had just picked it up.  I'm not sure what my face said back to her, but she quickly said, "Just joking" and gave me my suitcase.  You really start thinking about what you had in there and how easy or hard it will be to replace.  When I got back with my suitcase I called the Auto Club which came to start my mom's car and then on his advice, drove it for 45 minutes.

There were a couple of other little things I had to redo - fix one of the toilets, and get the 'lost wallet' charge off one of my mom's credit cards.  I'd already done that last November, but it was on the January bill again.

And VISA declined a purchase while we were in Seattle.  I guess I like that they're noticing when we aren't where we normally are and they fixed it when I called. I told them we'd be in LA.  But today, J got turned down again.   One more call to get back to the beginning. He said our Seattle update didn't get updated.  When I asked what that meant, he said it wasn't recorded.  We've had a pretty regular pattern of being in LA this last year and shopping at that market.  It's not part of our pattern that they should be able to see from our billing record.  Guess they aren't as sophisticated as they'd like us to believe. 

Meanwhile, J spent Thursday sleeping and Friday was my turn - no pains or queasiness for me, just depleted.  Flu?  Maybe.  J had a flu shot this year, but I didn't. 


But there were some upsides.  OP, who came out in the evening to get his suitcase (I offered to take it to him, but he declined), turned out to be a very nice person who's been to 49 states, except you-know-which-one.  I told him I'd pick him up at the airport when he comes.

And while I was driving the car to charge up the battery, I heard a phenomenal book review of Richard Powers' new book, Orpheo on KCRW's Bookworm.   Reviewer, Michale Silverblatt, engaged Powers at a level commensurate with the complexity of the themes in the book.  I posted in 2007 about Powers' The Echo Maker, an incredible book that interweaves the ancient migration pattern built into the genetic memory of sandhill cranes and the memory problems caused by capgras syndrome. Do try the link to the interview.  [I know the link is just above, but I figure the easier I make it to link, the more likely someone will.]

I also learned, looking up Richard Powers, that our paths have crossed - he was a student at the International School in Bangkok while I was a Peace Corps volunteer in Thailand and he returned home to DeKalb, Illinois where my Peace Corps group had trained.  This was about the same time Robert Merton was electrocuted in Samut Prakan, just south of Bangkok.


My todo list from this post?

1.  Put my name and contact info on the outside of my carryons as well as things I check in.  I had a very distinctive name tag on my roll-on (thanks Carol), but it disappeared on the previous trip when it flew as check-in.  And I didn't replace it.  Even after discussion the check-in lady in Anchorage talked about someone who had her name clearly on the outside of everything and on the inside as well.  (I did have a photo of the suitcase.)

2.  Look for Richard Powers' Orpheo.

At the Chimp Stage

I’d say that Z, my granddaughter, is in the chimpanzee stage of walking.  She can do it on her own, but walking on her knees is still much faster and more certain.

Chimp Image from Konrad Wohte

At 13 months, she still doesn’t say much - “Row, Row” (as in "your boat"), “Bye,” “no” and a word that sounds identical when she points to her nose.  And 'papa.'  “Uh oh” when something falls. 

apple

But more interesting to me, is that her mom has been teaching her sign language and she signs for hat (as in put on my hat), apple, and milk.  She repeats hat over and over again, and she gives me that hat to put on her head, then she takes it off and starts all over again.  But it’s not nearly as annoying as it might be if she kept repeating 'hat' out loud. She also knows more.

hat

The links take you to Babysignlanguage.com.  


I found what looks like a pop psychology website that touts the benefits of signing with your baby.  Nothing wrong with it, but more opinion, less evidence. 

I also found a report on research that found signing did not speed up when babies talk.  But, it did quote Dr. Liz Kirk:

"Although babies learnt the gestures and used them to communicate long before they started talking, they did not learn the associated words any quicker than the non-gesturing babies, nor did they did they show enhanced language development."
However, of significant interest, the study's findings did reveal that mothers who gestured with their babies were more responsive to their babies' non-verbal clues and encouraged them to think of their baby as an individual with a mind. This has great potential in clinical situations where early gestures from babies or young children may provide timely interventions where there is risk of language delay or impairment."

This was a study of only 40 mothers and babies.  It makes sense that babies wouldn't learn to speak faster - they are learning two languages after all, and the sign language probably reduces the need to speak.  And I don't think the study looked at long term benefits.

I'd heard that sign language can be helpful working with autistic kids and found a brief overview on that. 



Z and I also spent a solid hour together one morning putting some furniture together -  opening the box, unpacking the pieces, putting trash back into the box, etc.  She was totally involved including putting tiny washers onto the bolts.  Even though it took her six or seven times, when she dropped the washer, she’d say “Uh oh” and look around until she found it and try again.

These encounters with Z are too short, but she does seem to recognize us as people she knows and there's little warming up time needed before her mom can leave her with us with no fuss.   Now we're back in LA. 

Words, Symbols, and Meanings - Some Examples

Reinterpretation of Jesus' Words

From a bumper sticker I saw today:

Almost, but not quite, painting pictures with words.

Cloudstreet  is this month's book club choice.  I couldn't find it at Loussac in Anchorage, but they had an Australian tv series that someone said was good.  I watched the six episode DVD, and as interesting as the visual experience was, there was a lot missing.  Aside from some more character development, I wanted to enjoy Winton's prose.  I'd read a previous Tim Winton novel - Dirt Music - which I enjoyed thoroughly.  So, when I found it in the library here on Bainbridge Island, I asked my daughter to check it out for me.  Here's why I like the writing.  Rather than just say, "no one in the hospital room moved for a long time"  he writes

"The woman and the daughter do not speak.  The crippled man does not stir.  The breeze comes in the window and stops the scene from turning into a painting."

Did you see the curtain move?  Or feel the breeze? Or see the painting of the three in the hospital room? 



When It Helps To Have Slow Witted Authorities

In the Foreword to an English version of Between Man and Man, philosopher Martin Buber wrote:

". . .The book appeared in Germany in 1936 - astonishingly, since it attacks the life-basis of totalitarianism.  The fact that it could be published with impunity is certainly to be explained from its not having been understood by the appropriate authorities."

Diaper Fashion

I did complain about the vapidity of baby clothes last year and even found an Ai Weiwei t-shirt for Z online.   But when I changed her diapers this afternoon, I looked a little more carefully at the pattern.  This is definitely not vapid, but skulls and crossbones?  OK, why not?

Alaska's Permanent Fund Dividend For Oil Companies - $2 a Barrel or $28?

Oil companies are making a huge fortune in Alaska.  They already were doing great before Governor Sean Parnell, with the help of the Alaska Redistricting Board, which broke the Bi-partisan coalition in the State Senate, got SB 21 passed this last session. It's like they have their own Permanent Fund Dividend from the state - a $2 billion dollar a year check.  And it's not even their oil.  It belongs to the current and future residents of Alaska.  Bet they don't spend much of their dividend in Alaska. 

Bill Weilochowski, Les Gara, and a few others have been trying to tell Alaskans this story for years.  Another person who's been on trying to get the story out a long time is Ray Metcalfe.  In an Alaska Dispatch article Feb. 14 Metcalfe spells it all out.


Metcalfe has two major points:

1.  BP is making only $2 a barrel in Iraq, but about $28 a barrel in Alaska
2.  Alaska media aren't covering this story because they fear losing oil company advertising.  

On April 28, 2009, Bloomberg Business & Financial News reported that BP makes less than $2 net profit for producing a barrel of oil in Iraq. On March 14, 2010, Petroleum News reported what BP's net profit was under ACES without bothering to mention that it calculated to a net profit of $28 per barrel on their total production. ConocoPhillips' annual report also demonstrates a $28 to $30 per barrel net profit from Alaska oil under ACES. But no news reporter or TV news show in Alaska has ever bothered to tell you how little Iraq pays to the same companies for the same service. 

Metcalfe also speculates about why BP doesn't increase production in Alaska:

In 1995, BP persuaded Congress to let it export North Slope crude, but before it got around to doing so, BP jumped on an unforeseen opportunity to buy Atlantic Richfield Co.'s West Coast refineries and retail gas stations. Arco's refineries were built specifically to refine North Slope crude. BP's purchase of Arco West Coast assets appears to have incentivized BP to abandon ideas of exporting and pursue the much more profitable business of refining its North Slope crude into products to retail in what were Arco's gas stations.
Controlling Alaska crude from the wellhead to the gas pump is very likely the most profitable cash cow BP has. When BP's North Slope production exceeded BP's ability to refine and retail on the West Coast, when BP's West Coast storage tanks nearly ran over, BP further demonstrated the high value BP places on its North Slope crude. Rather than sell its excess crude before returning its tankers to Valdez, BP retained possession, sending several tankers back to Alaska with half their load still in their hulls. Producing more North Slope oil than BP's refined products market share can absorb would likely require export and most certainly shorten the life of BP's Alaska cash cow. It is very likely that the size of BP's West Coast refined-product market share has a lot to do with the rate of North Slope production.

And he shows what BP was willing to do just to make $2 a barrel in Iraq:

In 2009, BP, through a competitive bid process, won the right to produce Iraq's largest oil field, the Rumaila field. The field was producing a little more than 900,000 barrels per day when BP took it over. Iraq only pays BP for actual costs for managing the original production. The contract requires BP to raise daily production to make a profit. As production increases, BP is paid for actual costs plus $2 for every barrel produced in excess of the original 900,000 barrels. Now that the cat's out of the bag, the new talking point for the other side is that it is unfair to compare BP's contracts with Iraq to Alaska because BP had no original capital outlay in Iraq. Unfortunately for the other side, history doesn't support their argument. BP discovered and developed Iraq's Rumaila oil field in 1953. Iraq gave BP the boot for taking too much of the profit in 1961. Fifty years later BP went back to Iraq, hat in hand, and offered to resume pumping Iraq's Rumaila field for $4 per barrel, and Iraq said no. Then BP offered to do it for $2 and Iraq said OK, but only on the increased production. BP's contract requires BP to bring the Rumaila field's production to 2.9 million barrels per day within six years. If they make it they will be making $4 million per day by year six. That's $1.460 Billion net profit per year.

And then, again, compares this to BP's Alaska situation.

At $28 per barrel profit under ACES in Alaska, it would only require the production of 143,000 barrels per day to make the same amount of money. This year the three big North Slope producers will produce about 500,000 BPD and under ACES would have taken home a combined net profit of about $5.1 billion. If SB 21 is not repealed, their combined net take-home will be closer to $7.3 billion.

He also puts BP's jobs promises into perspective:

On October 3, 2013, BP told the Fairbanks News-Miner that thanks to SB 21's tax cut BP will now create 200 new Slope jobs. A positive statement unless one calculates how many jobs the state of Alaska could have created with a billion or two. One billion dollars is enough to create 10,000 jobs that pay $100,000 per year; 2 billion could create 20,000 such jobs. Not many readers would think that a fair trade, but no reporter in Alaska has offered to make the connection for you. 

I guess when Metcalfe says 'no reporter in Alaska has offered to make the connections for you"  he wasn't talking about bloggers.  Because I made exactly that connection almost on November 3, 2013 - How Many Jobs Could You Create For $2 Billion?

For instance I did a post (can't find it though) on this theme showing that for $2 billion a year you could hire every unemployed Alaskan and give them each $30,000 a year for their labor.  Not a great salary, but it gives you a sense that there are probably great alternatives to what the oil companies DON'T promise to do. 

[I still can't find the original post - I even looked in the old drafts to see if it never got posted.  In it I showed you could hire all the unemployed in Alaska for $30,000 a year each, which I figured was a better deal that the oil companies would ever do with the money.]


Metcalfe doesn't offer much data on why the Alaskan media don't report on the gap between oil company profits and in Alaska and in Iraq.  He does point out that readers in other cities get reports comparing Alaska and Iraq oil profits.

The Associated Press Media Ethics, Standards of Principles, under Integrity, includes this line:

The newspaper should report the news without regard for its own interests, mindful of the need to disclose potential conflicts. It should not give favored news treatment to advertisers or special-interest groups.

I'm not sure how you'd prove this.  The Anchorage Daily News could argue it's staff cuts, not fears of losing advertising.  They could also point to articles that do report unfavorably on the oil industry.  But I agree with the premise in the article's headline -

There would be no arguments over oil taxes if Alaska's media were doing its job

Metcalfe, a former Republican legislator, does his homework and has been pretty much on the mark in past criticism of politicians and their ties to the oil companies in the past.

Not too many rational folks would allow a former  oil company lobbyist to negotiate on their behalf with the oil companies.  But Alaskans have allowed, former Conoco-Phillips lobbyist and now Governor Sean Parnell to do just that.

Enough Alaskans have signed a petition to repeal the SB 21 oil tax cut to get it onto the August ballot.   Can a group of citizens defeat big oil in the voting booth?  Stay tuned. 

Peter Brilliantly Captures His PD Falls

I've posted about Peter Dunlap-Shohl's Parkinson's Disease blog before.  Peter's work is a bridge helping people without PD understand what his world is like.  And I'm sure people with PD appreciate that someone has captured their world and put it out there for all to see.

His most recent post is about falls.  Here's a screenshot of part of one of the panels.

Click to enlarge and focus

It's Peter's genius to be able to use his cartooning skills to capture the frustration, but also talk about the physiology and physics of what's happening. 

Pre-Checked Through Security - So Much Easier

Well, actually, there was only one other person in the regular line.  But not having to take off my shoes, or take my computer out, or my toothpaste was nice.  We didn't even have to put our hands over our heads, just through the old security walk through. 

And it made me think how when the pain is reduced, it feels good, even if it is still a pain.  There was a time when your friends and family could walk you to the gate or wait for you there as you got off the plane. 

Back in those days, they fed you on the plane and there was leg room.  BUT, and a big BUT, people could smoke on the plane.  So awful.  Even when the put the smokers in the back it was still awful.  

We checked in four pieces today.  Part of the clutter war - taking our daughter's old things still stored in our garage.  Mostly books.  And some baby stuff from friends who's kids are a little older. 

Our houseguest has gotten comfortable in the house.  What a pleasure to have him.  When he's home for dinner, he won't let us clear the table or wash the dishes.  Sometimes I actually like to do those kinds of mindless tasks, but I can get used to this. 

We'll see our daughter and granddaughter and the guys in a few hours.  So I better post this.  Enjoy the weekend.  It's warmed back up into the twenties here in Anchorage and it's mostly cloudy, but I can see blue and it's not raining or snowing. 

Narco Bling and Doumentary Heaven Trove of Docs

Documentary Heaven  is a website I ran into that has hundreds of documentaries you can watch.  Actually I didn't count them and there could be over a thousand. 

Here's the loooong  list of all the documentaries.  I suspect you could find everything just trolling YouTube, but this makes it a lot easier. 

Here are several titles that were being highlighted.

Amish: A Secret Life

An intimate portrait of Amish family life and faith, this film opens up a world usually kept private. Miriam and David are Old Order Amish and photography is not permitted under the strict rules of the Amish church. So when they agree to open their home and their lives to the cameras, they embark on a journey which is not without risk. As the film unfolds, we learn exactly what is at stake for this family and why they wanted to share their lives and risk all.

The Wall Street Code 

A thrilling documentary about a genius algorithm builder who dared to stand up against Wall Street. Haim Bodek, aka The Algo Arms Dealer. 

From the makers of the much-praised Quants:  the Alchemists of Wall Street and Money & Speed: Inside the Black Box.  Now the long-awaited final episode of a trilogy in search of the winners and losers of the tech revolution on Wall Street.  Could mankind lose control of this increasingly complex system?

 I haven't seen the first two, but I did watch this one:

 Narco Bling

Mexico is at war, a war for control of its own country against a rich and powerful enemy the Mexican drug cartel. These narco traffickers live in a world of astonishing wealth and extravagance, this being said however they live in even more spectacular cruelty and violence. This film is about the criminal gangs that are earning billions from a seemingly endless flow of illegal drugs, most of which seem to end up in the United States. National Geographic explore this dark world, where of the the most wanted fugitives is also one of the most powerful people in the region. 

It's not something I didn't already know, but the details are staggering.  The amounts of money, how things work, the impact on the US.   I couldn't help thinking:  Why are are fighting in the Middle East, when a much bigger threat is along our border? 

In the movie there's a scene in prison (it's shown with cartoon drawings) where a drug lord is imprisoned.  It shows how all the prison guards are bribed with offers of money and a laptop showing pictures of their families. It seems no one says no.  And you know that we must be losing the war on drugs because enough people on our side of the border are also being bribed.

Watch for yourself;  it's only 44 minutes. It was shown in England in 2010 on National Geographic television.

[UPDATE  Feb 23:  Less than two weeks after I post this documentary on Joaquin Guzman, he's captured.  If I used the kind of logic of some blogs and cable news shows, I could claim credit for his capture.  You can read the update post on this with links to the LA Times article on the capture.]

Catching Up - Left Over LA Shots - 60 Chevy, Monarch, And Dry Landscape

We're getting ready to go south again.  A few days in Seattle to see our grand daughter (and, of course, our daughter and the rest of the gang) and then to visit my mom who has her 92nd birthday in two weeks.

I've been busy - did a workshop today on racism with people in a drug and alcohol rehabilitation program.  It went quite well.  Having a house guest is fun, and he's wonderful, but I spend a lot more time just talking than normally.

Also, haven't done an update on my Achilles heel.  Long story short - been to the podiatrist, physical therapy, new shoes and inserts, back to the podiatrist when it swelled up again, some steroid treatment.  I'm ok at the moment, but running is going to have to wait until it's had more time to heal completely.  It appears my minimalist shoes might have contributed.  As I wrote earlier, while they are great for something things, they do put more strain on the Achilles heal.

I'd been thinking about taking a weight training class at UAA, but didn't get around to.  But T, our houseguest, suggested I just get a pass for the semester, and so I've been to the weight room a couple of times now.  I feel so much better getting good vigorous exercise again.  But I do still see people running and get very jealous.

I don't have too much time to post today, but I thought I'd put up some left over pictures from LA.

LA is a car city, so I thought I'd give you some cars.  Next is a 1960 Chevy.  We had one of these.  I couldn't believe my parents were buying it, I was stoked.  And I couldn't help talking a picture of this one, shiny in the setting sun.

These cars used a lot of gas, but gas was 31 cents a gallon back then.  And cars today are 99% cleaner than in the 1960s.  So, cool as they might be, I'm not sure driving them around is a good idea.  Of course, I don't know what kinds of modifications they might have made, or not.  The little vehicles above make more sense today.



And then there are birds.  Well, only a few photos.

A murder of crows chasing away a red tailed hawk above my mom's house.

We saw this bird when we were hiking in Las Trancas canyon in the Malibu area with some friends.  It looked somewhat like a jay, but I wasn't quite sure.  It had a blue coat. 

And some colorful birds sitting on a wall not too far from my mom's.











And a monarch butterfly resting on a jade plant.





From a New York Times article that just went up, it looks like genetically modified corn and soybeans and pesticides are threatening this magnificent butterfly that migrates 1000 miles.

MEXICO CITY — Hoping to focus attention on the plight of the monarch butterfly at a North American summit meeting next week, a group of prominent scientists and writers urged the leaders of Mexico, the United States and Canada to commit to restoring the habitat that supports the insect’s extraordinary migration across the continent.

Calling the situation facing the butterfly “grim,” the group issued a letter that outlined a proposal to plant milkweed, the monarch caterpillar’s only food source, along its migratory route in Canada and the United States.

Milkweed has been disappearing from American fields over the past decade as farmers have switched to genetically modified corn and soybeans that are resistant to the herbicide glyphosate that kills other plants. At the same time, subsidies to produce corn for ethanol have increased, expanding the amount of land planted with corn by an estimated 25 percent since 2007.

Back to the Las Trancas canyon hike.  It was a beautiful day - sunny, but not hot.  These pictures will give a little sense of how dry things are down there.

 

There were guided horseback rides that we passed on the trail.  

And one more that shows how the urban landscape can look fairly pastoral as well.  There's a public golf course near my mom's and this is a late afternoon shot along the edge of the course.